回憶模算數

我相信大家都知道什麼叫做模算數，這在現代密碼學當中被非常廣泛的應用。
首先是模除法：對一個整數 a 模除 n 的結果為 a 除以 n 的餘數，記作

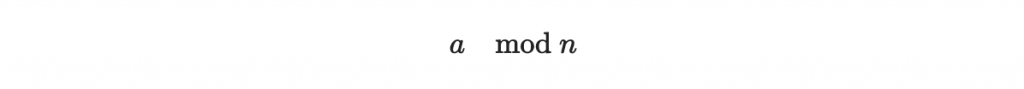
舉例來說：

接著，模加法：對兩個整數 a 與 b 在模 n 下做加法，結果為 (a+b) 除以 n 的餘數：

模乘法：對兩個整數 a 與 b 在模 n 下做乘法，結果為 (a * b) 除以 n 的餘數：

很間單對吧！好的，快樂時光結束。

在數學上，我們會使用環論（Ring Theory）來研究這樣的結構。簡要的說，如果你有一個集合，上面有加法，有乘法，並且滿足一些跟整數很像的性質（請參考ref），那我們就可以把這樣的「集合」、「加法」與「乘法」三個部件，稱作一個環。環裡面的加法，就叫做「環加法」，環裡面的乘法，就叫做「環乘法」。好！舉例！

整數（包含正負），配上你習以為常的加法與乘法，就可以稱作一個環！
環加法就是正常的加法，環乘法就是正常的乘法。

剛剛我們看到的模算數中，在模 13 的狀況下，

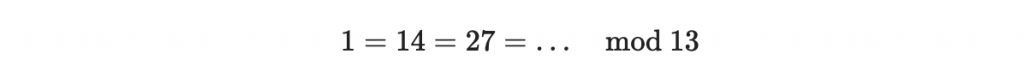
因此雖然整數有無限多個，『但是在模13的狀況下』，整個集合其實只剩下

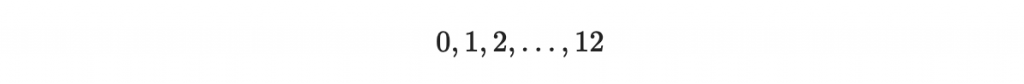
其他的數字都跟 0 到 12 中的某個數字相等，也就是相同的元素。

而此時的環加法就是

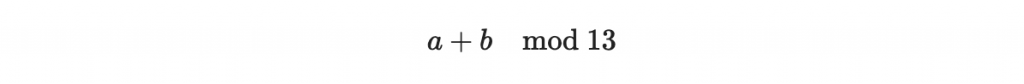
環乘法，就是

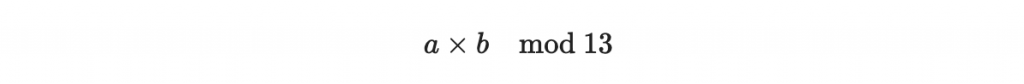
更廣義的說，在模 m 的視角下，我們其實在研究這樣的集合：

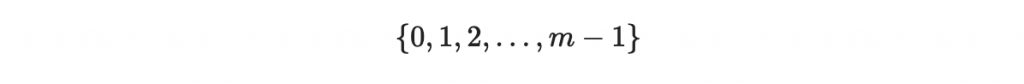
搭配上模加法與模乘法後，就變成模除 m 的環啦！

此時的環加法，就是

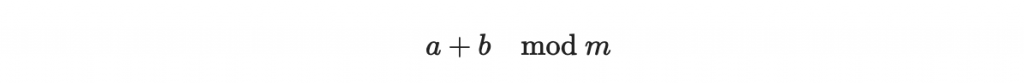
環乘法，就是

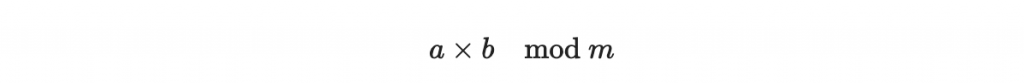
以上這些模除某數的環呢，中文會稱作「整數商環」或是「模除 m 的整數環」等等名稱，我們會使用一個特殊的符號來記：

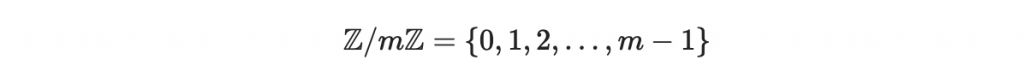
（開始可以用酷酷的符號來跟朋友賣弄了呢😀

其實數學上的環並不那麼狹隘，我們在未來幾天就可以看到「多項式環」、「多項式商環」等，並看看他們如何建構晶格密碼學。

SageMath 的威力展示

後，我們來看看 SageMath 的強大之處。SageMath 是一個建構在 Python 上的數學運算軟體，基本上 Python 能做的事情 SageMath 上都可做，會用 Python 就會用 SageMath。（上週我聽我學妹說現在高中生都會 C++，除了不禁感嘆現在升學環境是有多卷，也覺得我應該可以合理預設全世界的人都會用 Python （既使這兩個東西是毫無關係））

SageMath 最強大之處，就是它模組化定義了許多數學結構，例如上面提到整數商環，在 SageMath 裡面已經定義好了。

我們先呼叫「整數」這個類別：

# Sagemath
ZZ

Outputs: Integer Ring

Integer Ring 就是整數環的意思

接著，我們根據上面數學符號的寫法寫出「模除13的整數環」類別

m = 13
R = quotient(ZZ, m * ZZ)
R


Outputs: Ring of integers modulo 13

翻譯叫做，模除13的整數環

你可以用這個環來進行各種模算數運算：

比如說，試試模加法和模乘法：

a = R(7)
b = R(8)

# 此時 a 與 b 會是在 R 類別底下的元素：

print(a, type(a))
print(b, type(b))

# 來做環加法（模加法）、環乘法 （模乘法）
print(a + b)  # 7 + 8 mod 13
print(a * b)  # 7 * 8 mod 13


Outputs:
7 <class 'sage.rings.finite_rings.integer_mod.IntegerMod_int'>
8 <class 'sage.rings.finite_rings.integer_mod.IntegerMod_int'>
2
4

Takeaway

• 模除 m 的整數環中的環加法與環乘法就是以前學到的模加法與模乘法
• 我們可以用 SageMath 定義模除 m 的整數環，並建立該類別中的元素，進行環加法環乘法運算。

ref

DUMMIT, David Steven; FOOTE, Richard M. Abstract algebra. Hoboken: Wiley, 2004.
(Part II: Ring Theory)